WHITE PAPER

Peak Power in Non-Linear Microscopy: Unraveling the Rhetoric

Multiphoton Excitation (MPE) microscopy has brought femtosecond lasers into biological research labs for over 20 years now. Required wavelength ranges for excitation of various probes and laser powers compatible with low-damage invivo imaging have been well established. The appropriate pulse duration is however still the subject of discussion, individual preference, and different experimental conditions. This white paper provides useful information on femtosecond pulse propagation and management for non-linear imaging applications.

Introduction

Since the pioneering accomplishments of Denk et al. in two-photon laser scanning fluorescence microscopy, adoption of non-linear imaging and dedicated ultrafast lasers has greatly expanded [1]. Simultaneously, the capability, usability, and flexibility of laser technology have grown significantly.

Where initial work was dominated by complicated dye laser technology, Ti:Sapphire (Ti:S) lasers, fiber lasers, and OPO systems now offer a plethora of options in a turn-key format that are simple to use for a non-laser expert.

There are a number of key technical considerations when choosing a laser technology for multiphoton fluorescence excitation or photo-activation. Choosing a specific wavelength, or wavelength range, is a relatively simple process, driven by well-documented excitation cross-section spectra of the fluorescent probes of interest. What is more difficult is the selection of optimal power or peak power regimes.

There are several reasons for this difficulty, mostly because of the interplay between sample damage and fluorescence intensity on one hand and average power, peak power, and wavelength on the other hand. To further complicate the issue, in the literature one can find that MPE has been performed with wavelengths between 680 and 1,300 nm, pulses between 5 fs and 1- 2 ps, and energy/pulse at the sample between tens of picojoule and microjoules. Furthermore, modern lasers have the capability to deliver these short pulses right at the sample plane, by precompensating for linear dispersion in the optical train of a microscope system. As a result, there is room for some ambiguity and personal preferences in the choice, often determined by past experience that may or may not apply to a new experiment. The goal of this whitepaper is to provide some guidelines, based on data points taken from applications involving the Coherent Chameleon family.

Background: Non-Linear Fluorescence Excitation

We will assume firstly that reader has a basic background in the principles and advantages of multiphoton excitation of biological samples. Suffice to say, for a single pulse, the higher the instantaneous peak power, the greater the probability of 2 (or more) photon absorption. It follows there will be more fluorescence excitation, therefore more emission available for detection.

The peak power of a laser pulse, though strictly dependent on the exact temporal profile pulse, is generally written as follows:

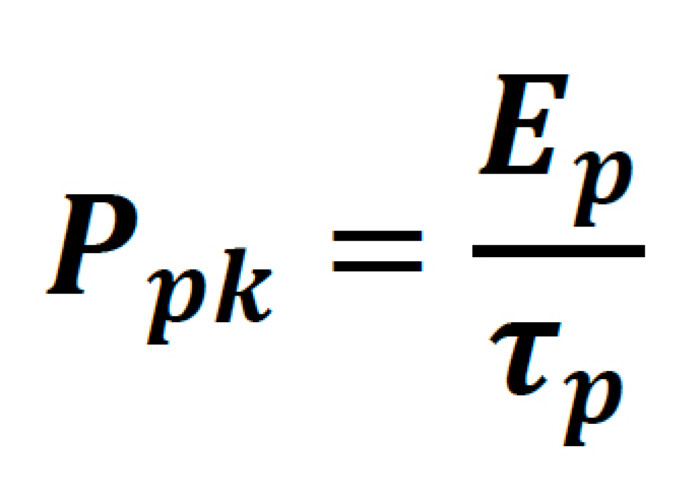
Where the pulse energy of the laser is:

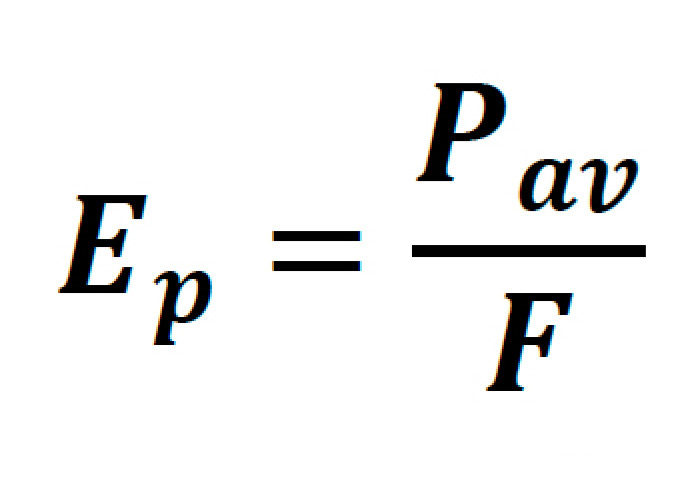
P_av being the average power of the laser, F representing the pulse repetition rate, and T_p representing the FWHM pulse duration.

For a laser scanning microscope, where the probes being excited have relatively short fluorescent lifetimes, the time-averaged emission is also dependent on the rate at which these pulses can be delivered to the sample. To this end, total fluorescence yield can be written as the product of the time-averaged power and peak power of the laser as follows:

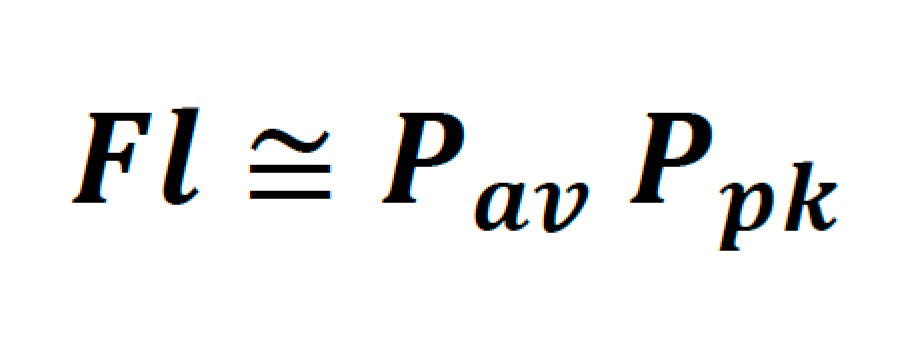
It is helpful to denote this in terms of parameters which are typically found on the datasheet of commercial laser systems, such as average power, pulse width, and repetition rate. Thus:

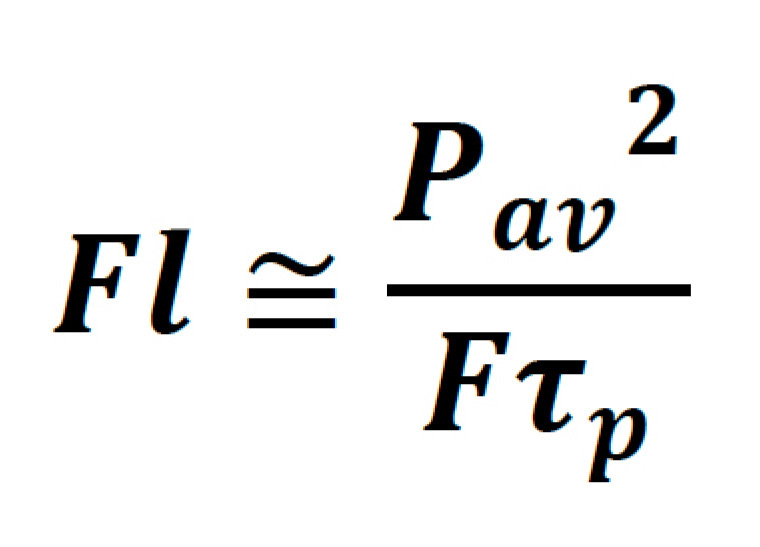
From here it is relatively simple to see which laser parameters can be adjusted to increase fluorescence from a sample. The catch is, not all of these parameters can be freely adjusted without compromises to sample viability, technical usability, and/or cost. These trade-offs will now be explored separately.

Photodamage in Multiphoton Microscopy

Despite many references and papers on photo-toxicity and linear photodamage in confocal imaging, there remain relatively few targeted, systematic, and quantitative studies exploring these dynamics for in-vivo and in-vitro MPE methods and sample types.

Some excellent insights and background can be gained from Hell et al. [2] and Koenig [3]. Most of the discussion in this section is derived from key works by the groups led by Hell [2], Piston [4], Neher [5], plus a theoretical analysis of photo bleaching mechanisms by Cheng et al. [6,7] A well-established cause of laser damage is the photo-thermal interaction. This occurs through linear absorption of the fundamental wavelength of the ultrafast laser source, or of any other CW or pulsed laser source. Linear absorption is highly dependent on the sample type and wavelength(s) used but is exclusively related to the average power absorbed by the sample, without any effect related to instantaneous peak power. Water, for example, dominant in most biological samples, has specific absorption lines in the near IR, and in general its absorption becomes more significant when using wavelengths above 1350 nm. The effects on a sample include local heating, and ultimately boiling of water in the sample, leading to cavitation. It should be noted that damage may however take place well before cavitation happens, i.e. when the local temperature raise exceeds the limit for cell viability. Hell et al. [8] have performed a simple but convincing evaluation of the temperature raise in specimens as determined only by linear water absorption. They showed that the typical average power used in MPE (~ 100 mW on the focal plane) determines a temperature raise < 1°C and concluded that in these samples thermal damage due to the laser power required for MPE is not an issue. It is however important to recognize that, in presence of strong absorption due to other species such as hemoglobin or melanin, the sample temperature can rise much more dramatically. For example, in human skin, 2P light penetration is often limited by melanin absorption [9]. In the presence of only linear effects, one could minimize these effects by decreasing the pulse duration and increasing the peak power that is beneficial to the non-linear excitation.

Photobleaching is a mechanism that leads to the rapid decrease of the fluorescent emission of a sample due to the degradation of the fluorescent species itself. Often the word photodamage is used to indicate photobleaching as the major cause of light-induced damage, although there may be other mechanisms that take place in the longer term. These mechanisms may be triggered by the change in chemistry related to photobleaching but may take place over longer periods of time than the timescale of photobleaching itself (a few seconds or tens of seconds). The mechanisms of photobleaching are complex and subject of active investigation in its various aspects. While photobleaching takes place both with 1- and 2-photon excitation, in case of 2-photon excitation, it is confined to the focal plane. It has been recognized that in presence of femtosecond pulses, photobleaching may increase with a power higher than 2, indicating a mix of 2-photon and 3-photon processes, or even higher-order processes [4, 5]. A simple explanation for the higher non-linearity of photobleaching is shown in Figure 1. Here a dye (or fluorescent protein) molecule is excited into the first singlet state S1 by 2-photon absorption; interaction with additional photons excite the molecule to even higher states via the process kb, possibly leading to a dissociation of the molecule. Alternatively, the singlet state excitation can be transferred via intersystem crossing to a triplet state T1 and this state can transfer its energy to a singlet oxygen state via k_o.

Independently from the probability of intersystem crossing, it is clear that the larger photon flux in MPE, especially at high peak powers, will increase the probability of 3- or 4-photon interaction leading to a highly non-linear term.

To summarize, increasing the laser power on a biological specimen eventually leads to photodamage that can be linear (absorption by water and other constituents) and non-linear (2P absorption leading to additional 1 or more photon absorption resulting in photobleaching). Thermal damage in MPE microscopy can be decreased by decreasing the pulse duration (and therefore the average power), but the resulting increase in peak power may lead to higher nonlinear photobleaching or other forms of damage. There then must be a trade-off between the decrease of thermal damage and the onset of non-linear effects.

Damage depends also on wavelength. A number of works has shown that increases in the excitation wavelength from 700-800 nm to 900-1,100 nm and even 1,250 nm is beneficial to the sample viability. Of course not all probes can be excited with long wavelengths, but it seems advantageous to excite fluorophores on the red-side of their excitation spectrum whenever possible. This is useful also because longer wavelengths undergo less scattering and therefore are conducive also to deeper imaging. Even better, longer wavelengths are more immune to dispersion, as discussed in the next sections. All these elements have pushed MPE towards the adoption of probes that can be excited in the safer 920-1,100 nm region.

While the assessment on longer wavelengths seems to be unanimous, selection of an ideal pulse duration remains more subjective, or even ideological. Before discussing it any further, it is useful to review the management of short pulses in a microscope system.

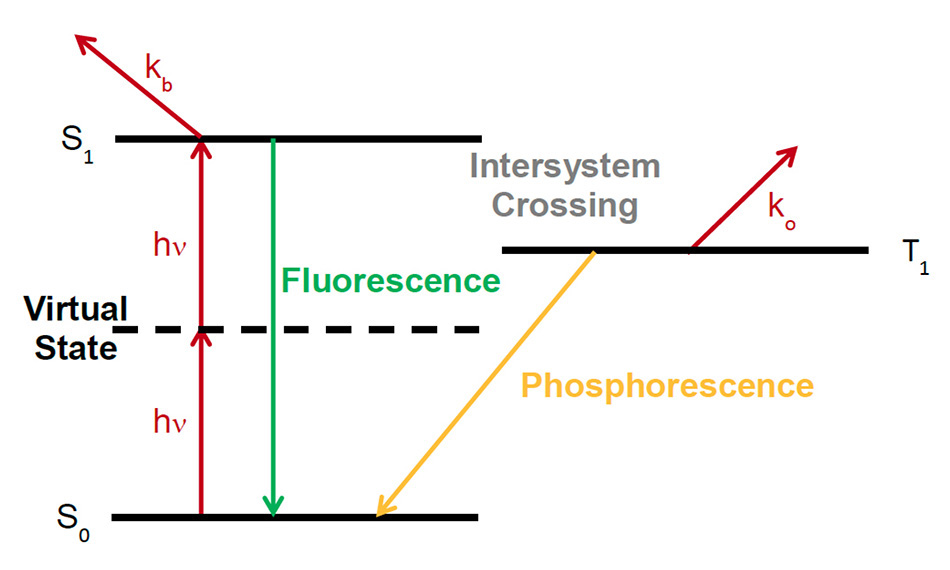
Figure 1: Photobleaching mechanisms via higher-order non-linear interactions, adapted from [7]

Managing the Propagation of Femtosecond Pulses

Ultrafast laser pulses of a particular temporal FWHM width have an intrinsic minimum frequency bandwidth, governed by their temporal pulse shape. For a hypersecant-shaped pulse (sech2) typical of commercial Ti:S lasers this is given by the following:

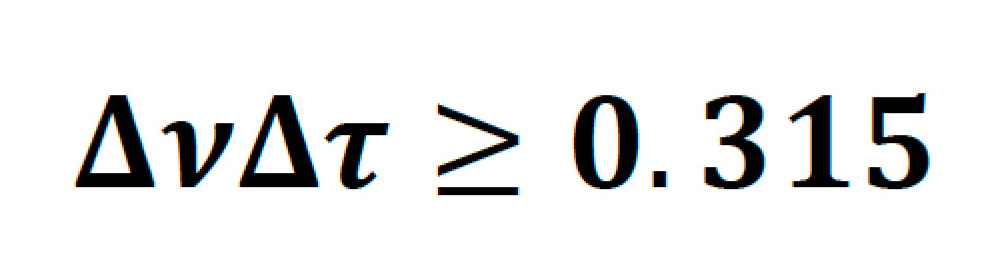
Or in terms of wavelength:

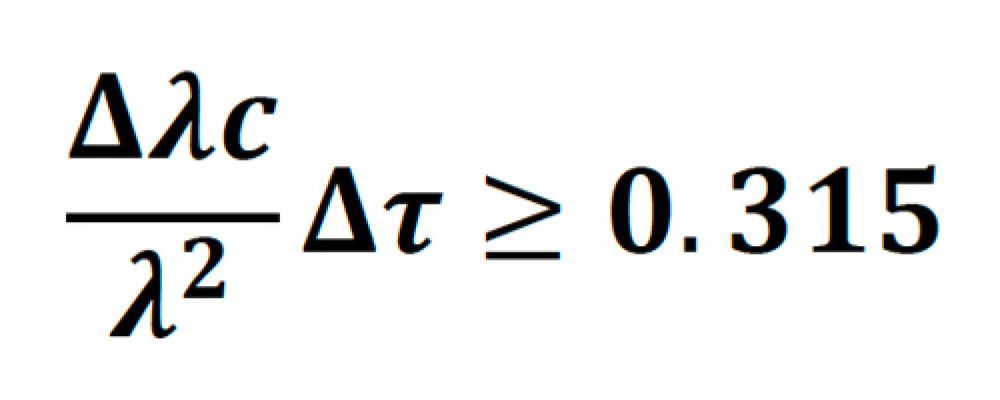
Sech₂ pulses, which have a time-bandwidth product of 0.315 are said to be transform-limited. As an example, a transform-limited 800 nm, 100 fs pulse, will have a bandwidth of 6.725 nm. In practice, a perfect pulse is very hard to achieve, and for Ti:S lasers the bandwidth is usually between 1.1-1.3 times higher than the transform limit.

The shorter a pulse becomes in width, the larger the bandwidth. This is important, because broad bandwidth pulses display a phenomenon known as group delay dispersion (GDD), when passed through a complex optical system such as a multiphoton microscope. Caused by the differing refractive index of an optical material for different wavelengths, this second-order effect means that the redder portion of the spectrum travels through a medium faster than the bluer portion, effectively lengthening the pulse. Such pulses are termed positively chirped. The larger the bandwidth of the pulse, the more the pulse lengthens.

The first generation of automated lasers specifically designed for multiphoton microscopy (Chameleon XR) operated at a pulse duration tailored around the typical GDD of microscope systems including a complex objective lens, a modulator, and a few other reflective elements. Figure 2 illustrates how a pulsewidth of about 140 fs is close to the optimum for a broad range of microscope GDDs.

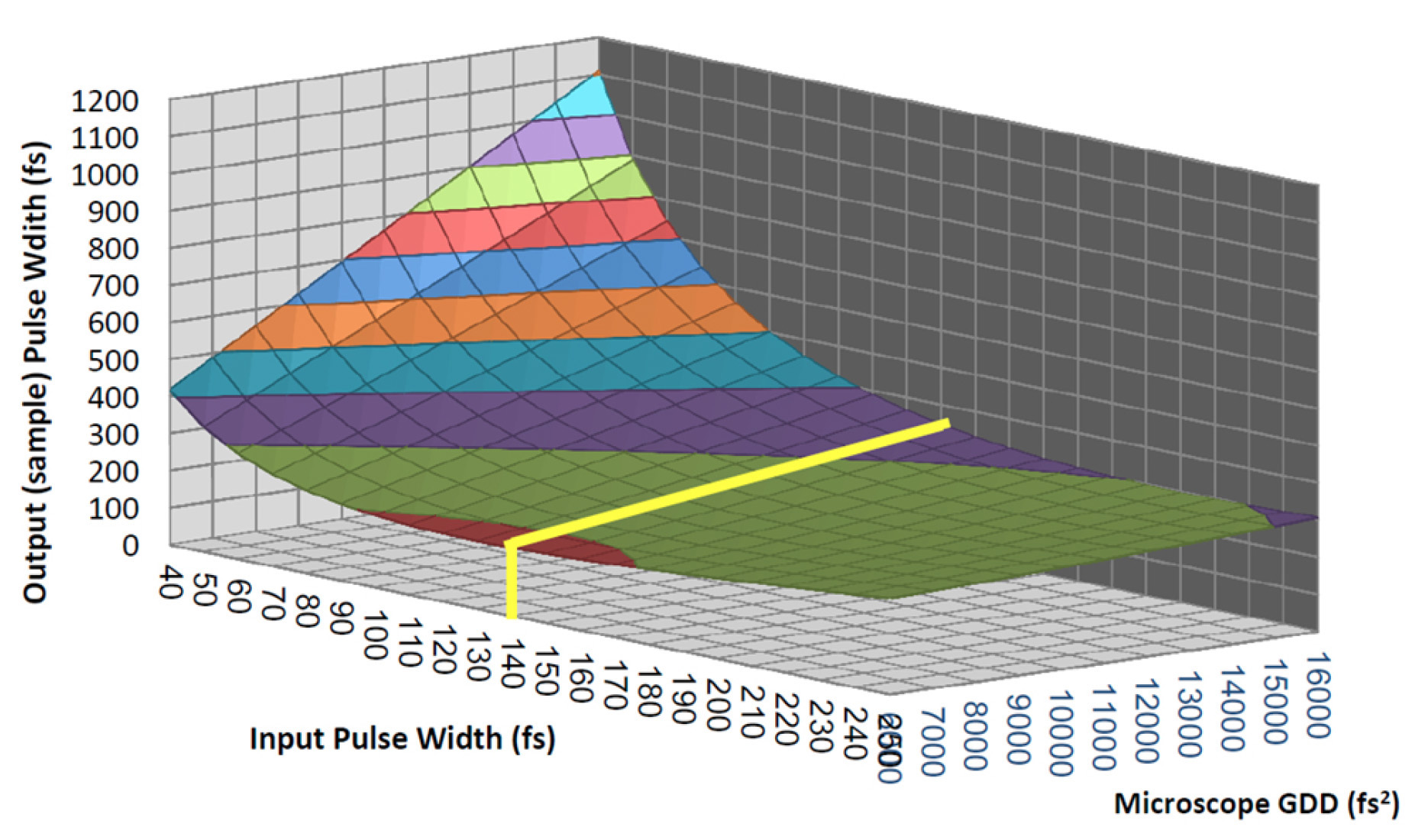
Figure 2: Pulse broadening for different input pulse durations and microscope complexities. It demonstrates how pulses of ~140 fs deliver the shortest pulse to the sample under the widest range of conditions.

The GDD of a microscope system is strongly wavelength dependent, and is typically much higher at shorter wavelengths, than at wavelengths beyond 1000 nm. The total GDD of a system is the product of GVD (Group Velocity dispersion) with the length of the material. See Figure 3 for typical GVD data. Note the high effect from TeO2, the most common material used in acousto-optic modulators.

Modestly complex microscopes have a total GDD below 8000 fs2 for wavelengths beyond 1050 nm, thus pulse broadening is not a strong concern for all but the very shortest of pulses. In fact, a pulsewidth of 200 fs, at 1100m will only stretch to ~230 fs under such conditions.

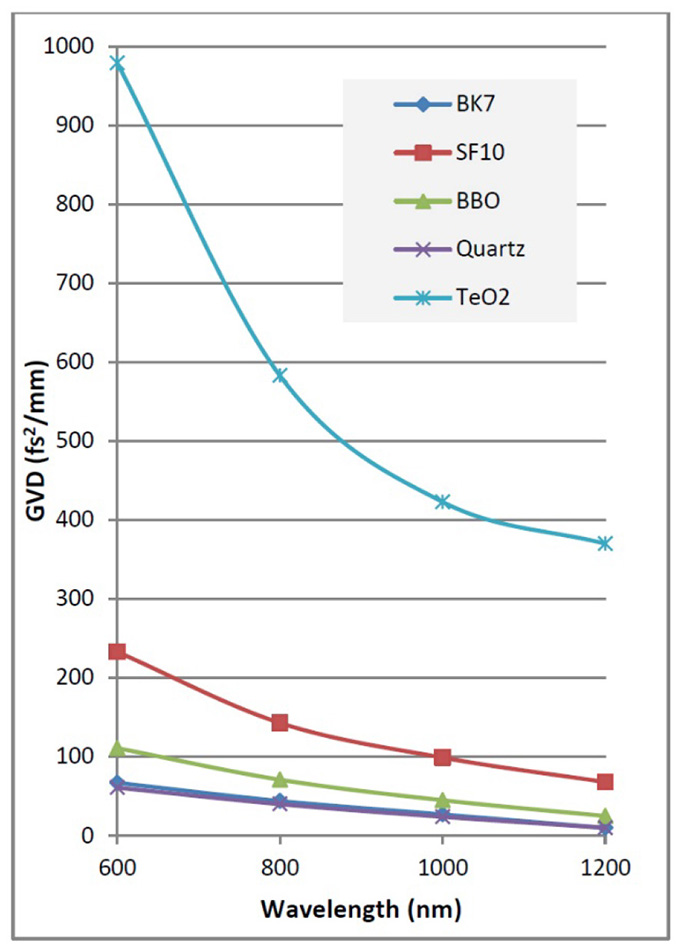
Figure 3: GVD for typical optical materials found in commercial 2P microscopes.

Precompensation for GDD in Femtosecond Lasers

It is clear from Figure 2 how the pulsewidth at the sample plane can increase dramatically with pulses less than 120 fs, when the total GDD is considerably higher than the 8000 fs2. This is quite common when a modulator (AOM or EOM) is included in the microscope system, a usual practice with most commercial MPE microscopes.

In an effort to circumvent the effect, skilled end-users and laser companies successfully devised methods to precompensate for the second-order GDD, by adding a negative chirp to the pulse before input to the optical system [10]. This can have a pronounced effect on image brightness whilst keeping the average laser power constant as exemplified in Figure 4.

Practical implementation of GDD precompensation can be done with chirped mirrors [11] as long as the wavelength being used is fixed and the amount or variability of negative chirp is limited. However, typical commercial, tunable Ti:S laser systems are now available with dispersion compensation, based on prism-pair compressors [12]. The system can be completely automated by motorizing the prism stages.

A user can set up a GDD curve tailored to their particular microscope, such that the pulse width at the sample plane may be minimized for any selected wavelength as shown in Figure 5.

The ability to dynamically change the pulsewidth can have benefits which include maximizing peak power, and in some cases it may be desirable to increase the pulsewidth when damage from phototoxicity of concern. Studies have shown that chirped (i.e. stretched) pulses can be an effective way to minimize such damage [2].

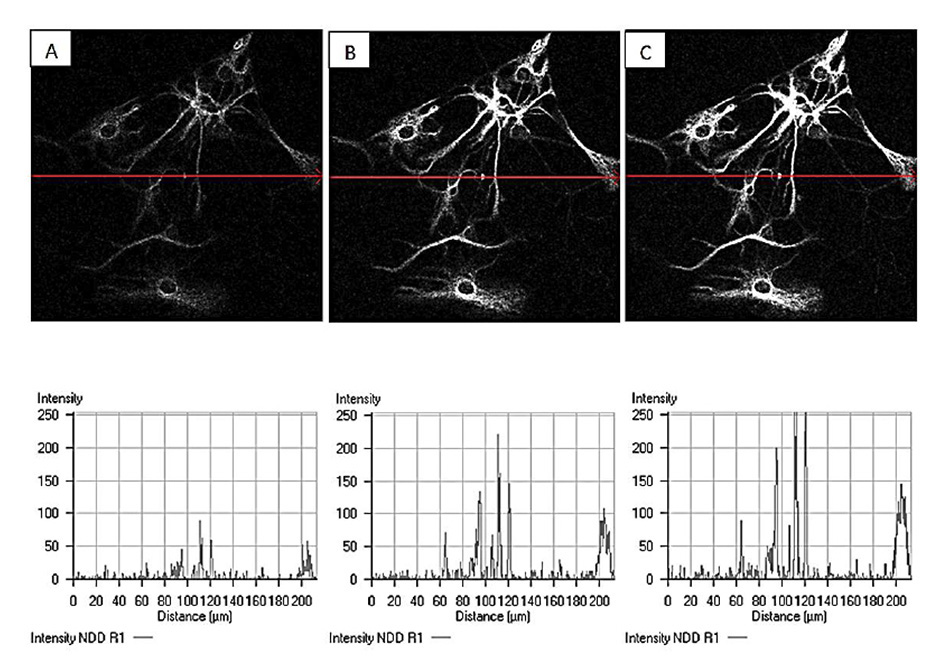
Figure 4: Example of increased image brightness through dispersion compensation. Laser power and detection gain are kept constant but GDD settings are varied for A: 0 fs2, B:10000 fs2, and C: 15000 fs2. 840 nm imaging of CY3 labeled Glial cells courtesy of Grenoble Institute of Neuroscience.

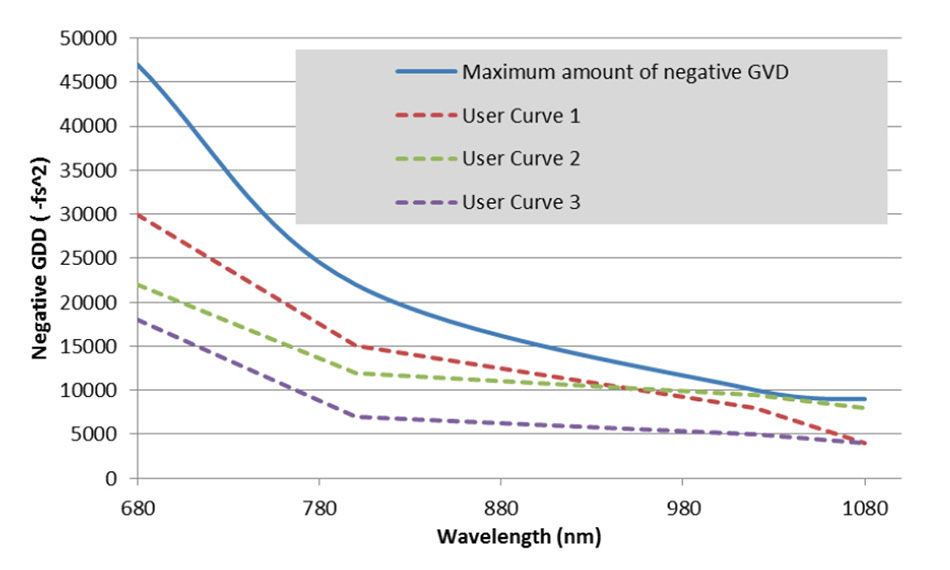
Figure 5: Negative GDD curves for dispersion compensating Ti:S lasers. Any value under the blue line can be programmed into a customized user curve.

There are practical considerations when selecting a laser with or without dispersion compensation. Considerations include the following:

The laser is more complex and larger. Prism-based compressors add at least 2-3 meters of optical path length to a laser output and despite elegant beam folding engineering, normally the precompensation section adds ~30 cm to the laser length.
The prisms themselves also add a certain amount of wavefront distortion to the beam, which in turn adds astigmatism to the beam. This potentially can affect the point spread function of an image. Best practice in laser build process and design also compensates for such effects.
There is some transmission loss through the prisms. Typically efficiencies are between 80 and 90%, depending on wavelength. For applications requiring very high average power this can be an important consideration.
It is important to set up the correct curve for the particular microscope configuration; otherwise it may be possible to inadvertently deliver longer rather than shorter pulses to the sample.

In general, lasers with pulses <100 fs will benefit from dispersion compensation in all but the very simplest of optical delivery trains. In fact, it could almost be said that such lasers need this facility. For lasers with pulses in the order of 140 fs, the benefits may not always outweigh the extra cost and size implications of the precompensation stage. However, it may lead to a greater flexibility of use for a wide variety of sample types.

If selecting a Ti:S laser with both dispersion compensation and very short pulses in the order of 70-80 fs, the correct setting of the precompensation prisms is particularly critical. Proper laser operation and optimization may be required at more regular intervals, see Figure 6 as an example.

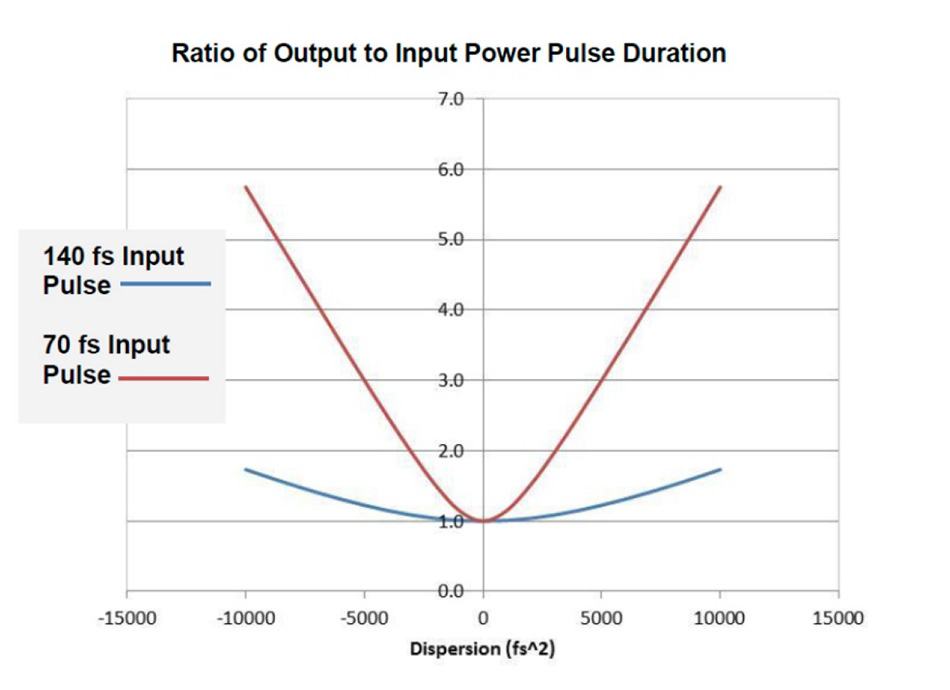
Figure 6: Sensitivity of GDD setting for typical Ti:S laser pulses. The shorter pulses require more care with GDD settings to ensure the best performance.

How Short is Too Short?

Given the market success of Ti:S lasers with automated dispersion compensation, it may lead one to ask why not make the laser pulse as short as possible? There are some important limitations that have conspired to limit the success of such ventures.

Within the scope of tunable lasers, limitations of optics design mean there is a trade-off in average power and tuning range. For example, a Ti:S laser with 140 fs can be tuned from 680 nm to 1080 nm. A 75 fs pulse, because of its inherently wider bandwidth, cannot tune so close to the edges of the fluorescence emission spectrum of Ti:S, thus is limited to ~1050 nm. This can be important for users looking to image red fluorescent proteins such as mCherry. In addition, as the laser spectrum exceeds 100 nm, its shape tends to diverge from a smooth Gaussian distribution, resulting in sub-optimal actual excitation at some spectral components.

The wider bandwidth of very short pulses should be also considered in the backdrop of the fluorescent marker being imaged. Two-photon cross-sections, though normally wider than their single photon counterparts, are usually <100 nm, and furthermore, the cross-section may depend on the actual pulse width [13, 14]. Ultra-broadband pulses have been employed more commonly to excite many probes at the same time rather than to address an individual marker. Possible exceptions are harmonic generation microscopy, where phase matching is relatively wavelength-independent, or excitation of quantum dots as these probes display bandwidth of hundreds of nanometers. In these cases use of very short pulses leads to high signal, nevertheless, sub-50 fs pulses in MPE have been only sporadically adopted.

Dispersion discussions thus far have focused only on second-order dispersion effects. Third-order dispersion (TOD) may also be a consideration for ultra-broad bandwidth pulses on more complicated microscope systems. This is the frequency dependence on the GDD, and is expressed in units of fs3. TOD is harder to model than GDD, and cannot be precompensated for with prisms alone. Discussion of this effect is beyond our current purpose but, as a general guide, lasers with pulses of approximately 30 fs or lower (or pulses with equivalent bandwidth) will need a more complicated system for phase control of the pulses for efficient multiphoton excitation [15].

Summary

Just about every non-linear microscopy application of general interest, inclusive of optogenetics and physiology for in vivo neuroscience can be addressed with femtosecond pulses in the range of 50-200 fs (from the laser source). Laser sources producing pulses below ~100 fs benefit from the use of precompensation in order to avoid loss of excitation due to peak power degradation. The need for precompensation is less stringent at wavelengths above 1 micron because the GDD of all optical materials strongly decreases at longer wavelengths. Independently on the wavelength used, increasing average power and/or peak power ultimately leads to linear (thermal) or non-linear damage respectively. A trade-off between the two types of damage exists but is different from sample to sample and also as a function of the wavelength. It also depends on the time-scale of the experimental observation. In general, the ability to access higher peak powers at the sample plane adds flexibility and capability to excite more fluorescence in samples with a high linear absorption and thus more susceptible to thermal damage. Furthermore, for users of very involved optical microscopes with high dispersion, adding precompensation of GDD will glean benefits in image brightness, which may well justify the added cost and complexity to the laser.