WHITEPAPER
Entwerfen kostengünstiger Freiformen
So entwerfen Sie kostengünstigere Freiformoptiken
Freiformoptiken (mit einer Form ohne Translations- oder Rotationssymmetrie) hatten einen erheblichen Einfluss auf luftgestützte Systeme und andere Anwendungen und sind ein Schlüsselfaktor für die kompakten weltraumgestützten Systeme, die insbesondere für Proliferated Low Earth Orbit (LEO) erforderlich sind. Der Grund dafür ist, dass ihre komplexen Formen die Herstellung optischer Systeme mit reduzierter physischer Größe und reduziertem Gewicht bei verbesserter Leistung ermöglichen. Aber die ausgefeilten Herstellungstechnologien, die Freiformen ermöglicht haben, führen auch zu Herausforderungen bei der Fertigung, die bei der Herstellung von traditionellen, rotationssymmetrischen sphärischen und asphärischen Optiken nicht auftreten.
Diese Herausforderungen können Hersteller erheblich beeinträchtigen und sie geben die damit verbundenen Kosten und technischen Risiken normalerweise an ihre Kunden weiter. Oder schlimmer noch, wenn die Hersteller dies im Vorfeld in Rechnung stellen und die Kundenaufträge dadurch gefährden, dass sie nicht spezifikations- oder termingerecht liefern können. Dieses Dokument soll Konstrukteuren von Optiken bei der konsistenten Erstellung von Freiformen unterstützen, die auf kostengünstige Weise leicht hergestellt werden können. Insbesondere stellt dies eine Messgröße dar, mit der die Herstellbarkeit und damit die Durchlaufzeit und die Kosten prognostiziert werden können.

Das Verhältnis von Oberflächenform zu Herstellbarkeit und Kosten
Das Ziel eines Herstellers ist es, eine optische Oberfläche herzustellen, die den beabsichtigten Konstruktionsvorgaben entspricht. Aber reale Herstellungsprozesse sind nicht perfekt, daher muss eine Konstruktion immer eine gewisse Toleranz für Fehler berücksichtigen. Und natürlich wird der Polierprozess umso einfacher, je größer die Konstruktionstoleranz für Fehler ist, was wiederum die Teilekosten und die Vorlaufzeit reduziert.
Für Hersteller von Freiformoptiken ist die am einfachsten zugängliche Methode zur Quantifizierung der Formgenauigkeit diejenige mit Fehlern bei niedriger und mittlerer räumlicher Frequenz. Insbesondere entsprechen niederfrequente Oberflächenfehler den traditionell verwendeten Maßen der Großserien-Formgenauigkeit für sphärische Optiken, wie z. B. Leistung, Unregelmäßigkeit und Zernike-Polynome. Fehler mit mittlerer räumlicher Frequenz (MSF) bestehen in einem kleineren physikalischen Maßstab und entsprechen (Rest-)Welligkeit und Tangentenfehler. Hochfrequenzfehler sind im Wesentlichen eher Oberflächenrauhigkeiten als Formfehler.
Was verursacht in Bezug auf das Design tendenziell Fehler bei der Herstellung im Bereich der niedrigen und mittleren räumlichen Frequenz? Mit anderen Worten, was kann ein Konstrukteur tun, um diese Fehler zu vermeiden oder zu minimieren und daher Designs zu erstellen, die von Natur aus einfacher herzustellen sind? Coherent, Inc. verfügt über jahrzehntelange Erfahrung bei der Herstellung von Freiformoptiken und hat festgestellt, dass einer der wichtigsten Faktoren, die die Herstellbarkeit von Freiformen beeinflussen, die Änderung der Krümmung der optischen Oberflächenform ist. Die Änderung der Krümmung ist insbesondere ein nützliches Ersatzmaß für die Herstellungskomplexität, da sie direkt mit die Polierzeit und die Testkomplexität beeinflussenden Prozessparametern korreliert.
Das nächste Diagramm fasst die Beziehung zwischen Oberflächenfehler (kombinierte niedrige und mittlere räumliche Frequenzen) und der Änderung der Krümmung für eine Anzahl verschiedener tatsächlicher optischer Komponenten zusammen. Es enthält Messungen von Optiken, die bei Coherent unter Verwendung verschiedener Produktionsverfahren und Substratmaterialien hergestellt wurden.
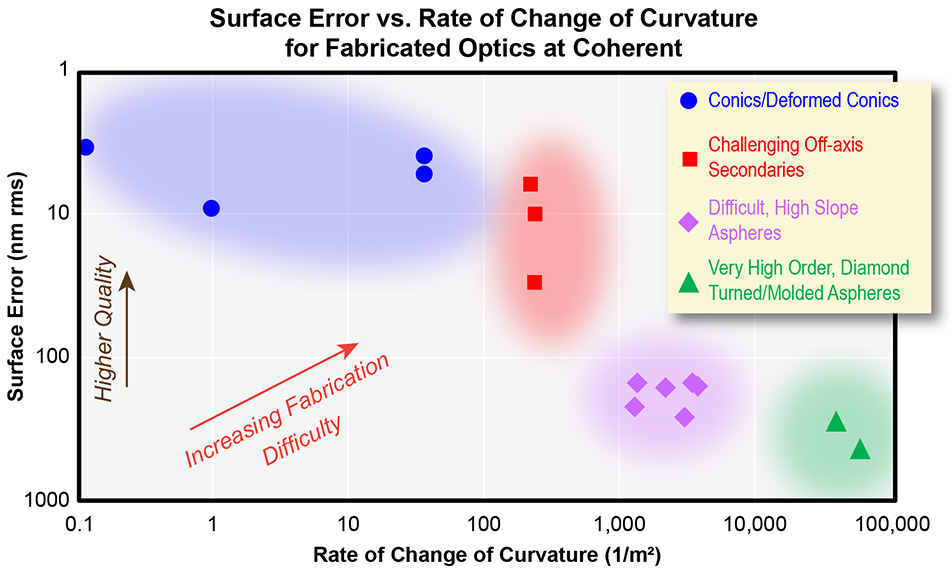
Die y-Achse des Diagramms zeigt den in vertikaler Richtung abnehmenden Oberflächenfehler. Je näher also ein Punkt am oberen Rand des Diagramms liegt, desto besser ist die Gesamtoberflächengenauigkeit. Auf der x-Achse ist die Änderung der Krümmung und nicht die Krümmung selbst aufgetragen. Beachten Sie, dass beide Achsen logarithmisch sind.
Die inhärente Herstellungsschwierigkeit nimmt von unten links (geringste Änderung der Krümmung und größter Oberflächenfehler) nach oben rechts (schnellste Änderung der Krümmung und geringster Oberflächenfehler) im Diagramm zu. Wie vorhersehbar, tendieren die tatsächlichen, gemessenen Daten von oben links nach unten rechts. Je höher nämlich die Änderung der Krümmung ist, desto größer ist der resultierende Oberflächenfehler in der fertigen Optik.
Was in dieser Grafik nicht zu sehen ist, ist der erforderliche Aufwand (z. B. Zeit) für ein bestimmtes Ergebnis. Und das ist der Schlüssel, da sich dies direkt in den Kosten niederschlägt. Es ist möglich, die Optiken, die im oberen rechten Quadranten des Diagramms liegen würden (z. B. „schwierige, stark geneigte Asphären”), mit einer höheren Oberflächenqualität als hier gezeigt herzustellen. Um dies in der Praxis zu erreichen, ist jedoch eine deutlich längere Herstellungszeit erforderlich; in der Folge verlängert sich die Vorlaufzeit und die Kosten steigen. Daher stellt die Grafik weniger das dar, was „machbar“ ist, als vielmehr das, was „kosteneffektiv“ ist.
„Je höher die Änderung der Krümmung ist, desto größer ist der resultierende Oberflächenfehler in der fertigen Optik. “
Ergebnisdiskussion
Dieses Diagramm stellt tatsächlich Daten mehrerer unterschiedlicher Arten von Komponenten dar, daher lohnt es sich, jede davon einzeln zu überprüfen, um die wichtigsten Erkenntnisse in jedem System zu verstehen.
Kegelschnitte/verformte Kegelschnitte
Diese relativ „einfachen” asphärischen Formen sind am leichtesten herzustellen. Die hier gezeigten Datenpunkte gelten für optische Komponenten im Größenbereich von 30 mm bis 1,5 m. Optiken aus praktisch jedem Substratmaterial, einschließlich Aluminium und Silizium, können mit einem geringen Restabweichungsfehler in diesem Änderungsbereich der Krümmung hergestellt werden. Die Herstellung von Optiken in diesem Bereich beinhaltet typischerweise keine signifikanten Kompromisse bei Form, Rauheit oder MSF-Fehlern, um die nominelle Form zu erhalten. Diese Oberflächen können im Allgemeinen in nahezu jeder gewünschten Qualität hergestellt werden, solange die Änderung der Krümmung unter ~100/m² bleibt.
Herausfordernde konvexe Freiformen oder „Sekundärseiten" außerhalb der Achse
Diese Datenpunkte wurden für relativ kleine (≤ 50 mm Durchmesser), typischerweise konvexe Spiegel aus Aluminium, Glas, Silizium und Siliziumkarbid ermittelt. Typischerweise als sekundärer Spiegel in vielen klassischen Teleskopdesigns verwendet, wird es zunehmend schwieriger, diese Klasse von Komponenten mit einem geringen Oberflächenfehler über einer Krümmungsänderung von etwa 250/m² herzustellen. Konvexe Spiegel können auch eine Herausforderung darstellen, da sie häufig mit einem geringen Freibord (dem Abstand von der Kante der freien Öffnung zur mechanischen Kante des Teils) spezifiziert sind und die Notwendigkeit eines schnellen Übergangs von der optischen Oberfläche zur mechanischen Kante nicht genügend Platz bietet, um das Polierwerkzeug zu stützen, wenn es sich um den Rand der freien Öffnung bewegt.
Schwierige, stark geneigte Asphären
Bei diesen Komponenten mit stärkerer Neigung (Änderung der Krümmung) müssen häufig Kompromisse zwischen Form, Rauheit und MSF eingegangen werden, um ein Teil entsprechend der angemessenen Vorgaben von Zeit und Kostenbeschränkungen zu erhalten. Auch wenn es möglich ist, den Oberflächenfehler (insbesondere MSF) für diese Klasse von Optiken zu verbessern, sind die hierzu erforderlichen Herstellungstechniken (aufgrund der starken Neigung) begrenzter. Daher können strenge Spezifikationen die Kosten schnell in die Höhe treiben.
Diamantgedrehte/geformte Asphären sehr hoher Anforderung
Teile mit Formen, die eine Krümmungsänderung in diesem Bereich (>10.000/m²) aufweisen, werden typischerweise unter Verwendung von Techniken wie Diamantdrehen und -formen anstelle des herkömmlichen Polierens hergestellt. Insbesondere das Diamantdrehverfahren erzeugt oft sogenannte „Farbe” in einer Optik.
Zusammenfassung
Die in diesem Dokument präsentierten Daten sind ein Versuch zu ermitteln, was „Bewährte Verfahren“ für das Entwerfen von Freiformoptiken sind. Mit dem anhaltenden Fokus auf die Entwicklung optischer Teleskopbaugruppen für stark auf Freiformoptiken angewiesene Proliferated Low Earth Orbits (LEOs), werden die Qualitätsanforderungen immer anspruchsvoller; dies gilt gleichermaßen für das Einhalten der Vorgaben im Hinblick auf Kosten und Termine. Die hier gezeigte Grafik stellt keineswegs alles dar, was erreicht werden kann – bei unbegrenztem Zeit- und Arbeitsaufwand. Vielmehr versucht sie, einige Grenzen für das zu definieren, was leicht herstellbar ist, und die Faktoren stärker herauszustellen, für die es am wahrscheinlichsten ist, dass sie die Komponentenkosten oder die Vorlaufzeit in die Höhe treiben. Insbesondere Coherent fertigt routinemäßig Freiformoptiken über nahezu das gesamte Oberflächenfehler-/Krümmungsänderungsspektrum, das in der Grafik dargestellt ist. Ein Hauptziel besteht darin, Kunden dabei zu unterstützen, ihre Designziele so kostengünstig und zeitnah wie möglich zu erreichen, und wir hoffen, dass diese Diskussion diesem Ziel zugute kommt. Unternehmen mit komplexen Anforderungen an Freiformoptiken sollten sich früh in der Designphase mit ihrem Optikpartner treffen, um Effizienzen oder Kompromisse zu identifizieren, die Kostenüberschreitungen und Projektverzögerungen reduzieren könnten.
Sehen Sie sich unsere vollständigen Fertigungs- und Beschichtungskapazitäten an